| |
Логико-вероятностное исчисление (ЛВИ) – специальный раздел дискретной математики, в котором установлены четкие правила замещения логических аргументов (xi) в функциях алгебры логики (ФАЛ) – y(x1,...,xn) вероятностями их истинности Р{xi=1} и логических операций: конъюнкции (Λ), дизъюнкции (V), отрицания ( ¬ ) арифметическими операциями: умножения (х), сложения ( + ), вычитания ( - ).
Нормированная булевская алгебра измеримых подмножеств сегмента [0,1] послужила образцом построения аксиоматики вероятностей А.Н. Колмогорова (1929).
Еще раньше (1917) С.Н. Бернштейн предложил рассматривать сами вероятности событий xi как вероятности истинных названных высказываний Р{xi=1}.
Булева алгебра – это алгебраическая система, которая в зависимости от обстоятельств может быть интерпретирована либо как система событий, либо как система высказываний. Аксиомы булевой алгебры выражают то общее, что роднит “события” и “высказывания”.
Взаимные переходы от языка высказываний к языку событий и обратно совершаются таким образом, что каждому событию сопоставляется событие, состоящее в том, что оно оказалось истинным.
Вероятностная функция (ВФ) – это вероятность истинности функции алгебры логики, т.е.
P{ у(x1 ,....,xn)=1}.
Событийная теории вероятностей и математическая логика в случае исключения высказываний являются дистрибутивными структурами, и поэтому такое определение вероятностной функции соответствует определению А.Н. Колмогорова [1].
Прямое замещение истинностных значений высказываний в функциях работоспособности (в теории надежности) или в функциях опасности (в теории безопасности) до разработки логико-вероятностного исчисления было возможно только для систем, имеющих простую структуру: последовательную, параллельную или древовидную.
Для систем, имеющих сложную структуру (мостиковую, сетевую и др.), прямое замещение истинностных значений высказываний xi на их вероятности
Р{xi=1} требует специальных преобразований ФАЛ, т.е. алгоритмов, которые и были разработаны российскими учеными научной школы логико-вероятностных методов (ЛВМ) для исследования проблем надежности, живучести и безопасности (НЖБ) структурно-сложных систем (ССС) [2].
Следует подчеркнуть существенную разницу между ЛВИ и вероятностной логикой, длительное время рассматривавшиеся чуть ли не как синонимы.
Вероятностная логика (ВЛ) – это логика, исследующая высказывания, принимающие не только два значения (истина и ложь), а множество степеней правдоподобия, т.е. высказывания, истинностные значения которых заключены в промежутке между истиной и ложью
0 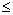 xi xi 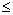 1. 1.
Поскольку в вероятностной логике анализируются высказывания более чем двух истинностных значений, она является одним из видов многозначной логики.
Отсутствие до сих пор какого-либо упоминания о ЛВИ и ВЛ в “Математическом энциклопедическом словаре (1988) или в книге “Математика. Большой энциклопедический словарь” [Гл. ред. Б.В. Прохоров, 3-е изд., М.: БЭС., 1998], а также существующие сомнения в ряде источников, требуют полнее и доказательнее высказаться о ЛВИ.
Объединяя в ЛВИ полную определенность (при формализации задачи) с неопределенностью состояния (каждого элемента системы), это не отрицающие друг друга начала, а удачно дополняющие компоненты, обеспечивающие прозрачность и точность расчетов [3].
(См.подроднее - Феномен ЛВИ).
Литература:
1. Колмогоров А.Н. Основные понятия теории вероятностей // “Наука”, М, 1974, с. 36.
2. Ленинградская научная школа логико-вероятностных методов исследования надежности и безопасности структурно-сложных систем. // Наука Санкт-Петербурга и морская мощь России, “Наука”, СПб, 2002, т. 2, с. 797-811.
3. Рябинин И.А. Логико-вероятностное исчисление как аппарат исследования надежности и безопасности структурно-сложных систем”. // АиТ, “Наука”, М, 2003, № 7, с. 178-186.
|
|